Question

Claire bought 5 kg of apples and 2 kg of bananas and paid altogether $22 Dale bought 4 kg of apples and 6 kg of bananas and paid altogether $33 Use matrices to find the cost of 1 kg of bananas

Answer 1

$3.5

Step-by-step explanation:

Let the cost of 1 kg of apples = x

Let the cost of 1 kg of bananas​ =y

Claire bought 5 kg of apples and 2 kg of bananas and paid altogether $22.

`5x+2y=22`

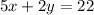
Dale bought 4 kg of apples and 6 kg of bananas and paid altogether $33.

`4x+6y=33`

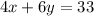
We set up the system of linear equations as a matrix below:

`\begin{bmatrix}{5} & {2} & \\ {4} & {6} & {}{}\end{bmatrix}\begin{bmatrix}{x} & \\ {y} & {}{}\end{bmatrix}=\begin{bmatrix}{22} & \\ {33} & {}{}\end{bmatrix}`

We then solve for the variables x and y as follows.

`\begin{gathered} \begin{bmatrix}{x} & \\ {y} & {}{}\end{bmatrix}=\begin{bmatrix}{5} & {2} & \\ {4} & {6} & {}{}\end{bmatrix}^(-1)\begin{bmatrix}{22} & \\ {33} & {}{}\end{bmatrix} \\ =(1)/(30-8)\begin{bmatrix}{6} & {-2} & \\ {-4} & {5} & {}{}\end{bmatrix}\begin{bmatrix}{22} & \\ {33} & {}{}\end{bmatrix} \\ =(1)/(22)\begin{bmatrix}{6} & {-2} & \\ {-4} & {5} & {}{}\end{bmatrix}\begin{bmatrix}{22} & \\ {33} & {}{}\end{bmatrix} \end{gathered}`

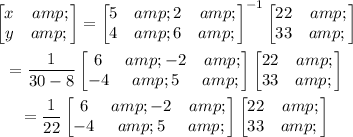
We proceed to simplify further.

`\begin{gathered} =\begin{bmatrix}{(6)/(22)} & {-(2)/(22)} & \\ {-(4)/(22)} & {(5)/(22)} & {}{}\end{bmatrix}\begin{bmatrix}{22} & \\ {33} & {}{}\end{bmatrix} \\ =\begin{bmatrix}{(6)/(22)*22-(2)/(22)*33} & {} & \\ {(-4)/(22)*22+(5)/(22)*33} & & {}{}\end{bmatrix} \\ =\begin{bmatrix}{6-3} & {} & \\ {-4+7.5} & & {}{}\end{bmatrix} \\ =\begin{bmatrix}{3} & {} & \\ {3.5} & & {}{}\end{bmatrix} \end{gathered}`

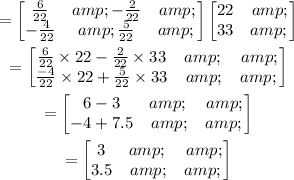
Therefore:

x=3 and y=3.5.

The cost of 1 kg of bananas​ is $3.5.