Answer:
$3.5
Step-by-step explanation:
Let the cost of 1 kg of apples = x
Let the cost of 1 kg of bananas =y
Claire bought 5 kg of apples and 2 kg of bananas and paid altogether $22.
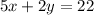
Dale bought 4 kg of apples and 6 kg of bananas and paid altogether $33.
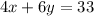
We set up the system of linear equations as a matrix below:
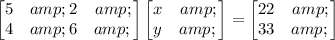
We then solve for the variables x and y as follows.
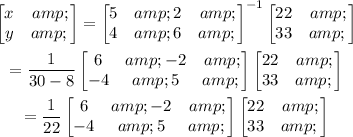
We proceed to simplify further.
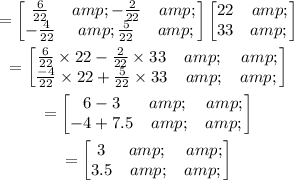
Therefore:
x=3 and y=3.5.
The cost of 1 kg of bananas is $3.5.