We have a game like the one described in the question and we have to calculate the expected payoff, which is equal to the sum of the possible outcomes weighted by the probability of that outcome.
In this case we have two outcomes:
1) We get an odd number and we win $26 (W=26).
2) We get an even number and we get $0 (W=0).
To calculate the probabilities of each oucome we have to know the proportion of odd an even numbers in the list of 1 to 50. We have a total of 50 numbers, rom which 25 are odd numbers and 25 are even numbers, so the probability of each outcome can be calculated as the relative frequency of each category:
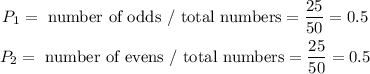
Then, we can calculate the expected payoff as:
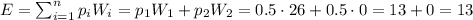
p_i: probability of outcome i.
W_i: prize when outcome i happens.
Then, the expected payoff for this game is $13.
Answer: the expected payoff for this game is $13.