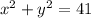Question

Find the standard form of the equation of the circle having the following properties:Center at the originContaining the point (-5,4)Type the standard form of the equation of this circle.

Answer 1

Equation of a circle in standard form:

`(x-h)^2+(y-k)^2=r^2`

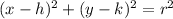
(h,k) is the center of the circle

r is the radius

For the given circle:

Use the center and the given point to find the radius: the radius is the distance from the center to any point in the circumference.

Distance between two points:

`d=\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2}`
`\begin{gathered} (0,0) \\ (-5,4) \\ \\ r=\sqrt[]{(-5-0)^2+(4-0)^2} \\ r=\sqrt[]{(-5)^2+4^2} \\ r=\sqrt[]{25+16} \\ r=\sqrt[]{41} \end{gathered}`

Use the center (0,0) (the origin) and the rafius to write the equation of the circle:

`\begin{gathered} (x-0)^2+(y-0)^2=(\sqrt[]{41})^2 \\ \\ x^2+y^2=41 \end{gathered}`

Then, the equation of the given circle in standard form is:

`x^2+y^2=41`