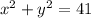Equation of a circle in standard form:
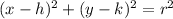
(h,k) is the center of the circle
r is the radius
For the given circle:
Use the center and the given point to find the radius: the radius is the distance from the center to any point in the circumference.
Distance between two points:
![d=\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2}](https://img.qammunity.org/2023/formulas/mathematics/college/be685jmxw05hm2tq94m5iuge2xjynn1hfn.png)
![\begin{gathered} (0,0) \\ (-5,4) \\ \\ r=\sqrt[]{(-5-0)^2+(4-0)^2} \\ r=\sqrt[]{(-5)^2+4^2} \\ r=\sqrt[]{25+16} \\ r=\sqrt[]{41} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/he9hkm4457qe3is64oe73i9flxgc26k4m1.png)
Use the center (0,0) (the origin) and the rafius to write the equation of the circle:
![\begin{gathered} (x-0)^2+(y-0)^2=(\sqrt[]{41})^2 \\ \\ x^2+y^2=41 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/um48lc3bjq5bemg82p4ht3og9x1osx9zqe.png)
Then, the equation of the given circle in standard form is: