Let x be the random representing the weights of the peaches produced by the company. Since the weights are normally distributed and the population mean and standard deviation are known, we would apply the formula,
z = (x - mean)/standard deviation
From the information given,
mean = 14
standard deviation = 0.4
For the weights to be more than 12.6 ounce, the equation would be
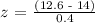
z = -3.5
Looking at the normal distribution table, the probability corresponding to the z score of - 3.5 is 0.00023
Since we want to determine propability for the weights greater than 12.6 ounce, the required probability would be
1 - 0.00023 = 0.99977
Given that the total number of peaches is 1000, the number of peaches expected to have weights more than 12.6 ounce is
0.99977 * 1000 = 999.77
Rounding to the nearest whole number, it becomes 1000
The number of peaches expected to have weights more than 12.6 ounce is approximately 1000