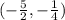Question

Which are the intercept points and vertex point for the function ƒ(x) = x^2 + 5x + 6?

Answer 1

The intercept points are:

`\begin{gathered} (-3,0) \\ (-2,0) \end{gathered}`

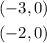
The vertex is:

`(-(5)/(2),-(1)/(4))`

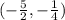
Explanation:

To find the intercept points, we equal the function to zero and solve for x, as following:

`\begin{gathered} x^2+5x+6=0 \\ \rightarrow(x+3)(x+2)=0 \\ \\ \rightarrow x+3=0\Rightarrow x_1=-3 \\ \\ \rightarrow x+2=0\Rightarrow x_2=-2 \end{gathered}`

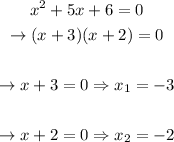
Now, we know that the intercept points have an x-value of -3 and -2. Since we're talking about intercepts, the y-values will be 0.

Therefore, we can conlcude that the intercept points are:

`\begin{gathered} (-3,0) \\ (-2,0) \end{gathered}`

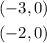
The vertex of any given quadratic function in the form:

`f(x)=ax^2+bx+c`

is:

`(-(b)/(2a),f(-(b)/(2a)))`

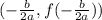
This way, for the given function, we'll have that the vertex point is:

`(-(5)/(2),-(1)/(4))`