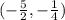Answer:
The intercept points are:
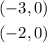
The vertex is:
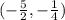
Explanation:
To find the intercept points, we equal the function to zero and solve for x, as following:
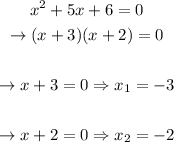
Now, we know that the intercept points have an x-value of -3 and -2. Since we're talking about intercepts, the y-values will be 0.
Therefore, we can conlcude that the intercept points are:
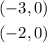
The vertex of any given quadratic function in the form:
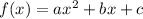
is:
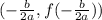
This way, for the given function, we'll have that the vertex point is: