Answer
For the arithmetic sequence,
15th term = 7,500
For the geometric sequence,
15th term = 19,131,876
We can see that the geometric sequence has the larger 15th term.
Step-by-step explanation
The general formula for an arithmetic progression is
f(n) = a + (n - 1)d
where
a = first term = 150
n = number of terms
d = common difference
= (Second term) - (First term)
= (Third term) - (Second term)
= Difference between consecutive terms
= 650 - 150
= 500
f(n) = 150 + (n - 1)500
f(n) = 150 + 500n - 500
f(n) = -350 + 500n
For the 15th term, n = 15
f(n) = -350 + 500n
f(15) = -350 + 500(15)
f(15) = -350 + 7500
f(15) = 7,150
For the geometric sequence,
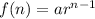
where
a = first term = 4
n = number of terms
r = common ratio
= (Second term)/(First term)
= (Third term)/(Second term)
= Ratio of consecutive terms
= (12/4)
= 3
For the 15th term, n = 15

Hope this Helps!!!