Question

One closed organ pipe has a length of 1.65 meters. When a second pipe is played at the same time, a beat note with a frequency of 1.8 hertz is heard. By how much is the second pipe too long? Include units in your answer.

Answer 1

Given,

The length of one of the organ pipes, L₁=1.65 m

The frequency of the beat note, f=1.8 Hz

The speed of sound is given by, v=343 m/s

The beat frequency is given by,

`\begin{gathered} f=|f_1-f_2| \\ =|(v)/(4L_1)-(v)/(4L_2)| \end{gathered}`

Where f₁ is the frequency of the 1st pipe, f₂ is the frequency of the second pipe, and L₂ is the length of the second pipe.

On rearranging the above equation,

`\begin{gathered} (4f)/(v)=|(1)/(L_1)-(1)/(L_2)| \\ \Rightarrow(1)/(L_2)=(1)/(L_1)-(4f)/(v) \\ =L_2=(1)/((1)/(L_1)-(4f)/(v)) \end{gathered}`

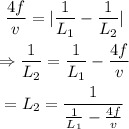
On substituting the known values,

`\begin{gathered} L_2=(1)/((1)/(1.65)-(4*1.8)/(343)) \\ =(1)/(0.61-0.02) \\ =1.7\text{ m} \end{gathered}`

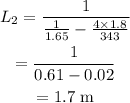
The difference in the length of the organ pipes is,

`\begin{gathered} \Delta L=L_2-L_1 \\ =1.7-1.65 \\ =0.05\text{ m} \end{gathered}`

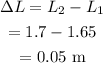
Therefore the second pipe is longer than the 1st pipe by 0.05 m