Given,
The length of one of the organ pipes, L₁=1.65 m
The frequency of the beat note, f=1.8 Hz
The speed of sound is given by, v=343 m/s
The beat frequency is given by,
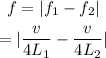
Where f₁ is the frequency of the 1st pipe, f₂ is the frequency of the second pipe, and L₂ is the length of the second pipe.
On rearranging the above equation,
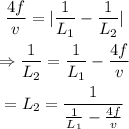
On substituting the known values,
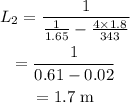
The difference in the length of the organ pipes is,
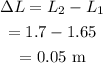
Therefore the second pipe is longer than the 1st pipe by 0.05 m