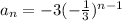In a geometric sequence each term is found by multiplying the previous term by a constant.
To find the nth term in a geometric sequence we use:

where a is the first term and r is the common ratio.
To find the common ratio we can divide the second term by the first:
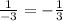
and the third one by the second:
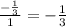
we notice that this in fact is the common ratio. Now we plug it in the formula above, therefore the geometric sequence is: