Answer:
Step-by-step explanation:
Given the function;
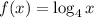
To be able to plot the graph of the above function, let's choose values for x and determine the corresponding f(x) values;
When x = 1;
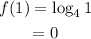
When x = 2;

When x = 4;
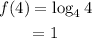
Let's go ahead and determine the inverse of f(x) following the below steps;
Step 1: Replace f(x) with y;
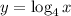
Step 2: Interchange the positions of x and y;
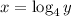
Step 3: Solve for y;

Step 4: Replace y with f^-1(x);
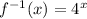
To graph the above function, let's also choose values for x and determine the corresponding f^-1(x) values;
When x = -4;
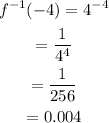
When x = 0;
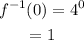
When x = 1;
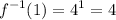
When x = 2;
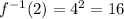
See the below graph of the f(x) and f^-1(x);