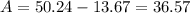#NAME?

Question

-what is the measure of arc AB-what is the length of arc AB-what is the area of the shaded section-what is the area of the unshaded section

Answer 1

Given Data:

The radius of the circle is, r = 4

The angle is, 98.

The measure of angle that an arc makes at the center of the circle of which it is a part. Therefore, the measure of the arc AB is 90.

The length of the arc AB can be calculated as,

`\begin{gathered} L=(98)/(360)*2*\pi* r \\ \text{ =}(98)/(360)*2*3.14*4 \\ \text{ =}6.84 \end{gathered}`

The area of the shaded section is equal to the area of the arc, which can be calculated as,

`\begin{gathered} A=(98)/(360)*\pi* r^2 \\ \text{ =}(98)/(360)*3.14*4^2 \\ \text{ =}13.67 \end{gathered}`

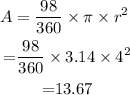
The area of the unshaded region can be calculated by subtracting the area of the arc from the area of the total circle. The area of the total circle is,

`A^(\prime)=\pi* r^2=3.14*4^2=50.24`

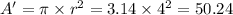
Therefore the area of the unshaded region can be calculated as,

`A=50.24-13.67=36.57`