Question

57. The graph of y=8-r represents the graph of y=r’ after(1) a vertical shift upwards of 8 units followed by a reflection in the x-axis.(2) a reflection in the x-axis followed by a vertical shift of 8 units upward.(3) a leftward shift of 8 units followed by a reflection in the y-axis.(4) a reflection across the x-axis followed by a rightward shift of 8 units.

Answer 1

Recall that the function represented by the graph of the function h(x) reflected over the x-axis is:

`-h(x)\text{.}`

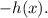
Also, recall that the graph represented by the graph of the function h(x) translated n units up is:

`h(x)+n\text{.}`

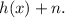
Therefore, the function represented by the graph of

`y=x^2`

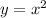
after a reflection over the x-axis followed by a translation of n units up is:

`y=-x^2+8.`

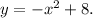
Using the commutative property of addition we get:

`y=8-x^2\text{.}`

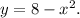
Answer: Second option.