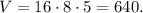(1) From the statement, we know that:
• the volume of a rectangular prism is:
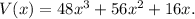
• and it also can be computed by:
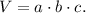
Where a, b and c are the lengths of the sides.
By factoring in the expression of V(x), we get:
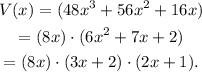
Comparing this result with the expression above, we see that the sides of the prism are:
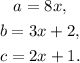
(2) Relacing the value x = 2 in the polynomial V(x), we get:

(3) Replacing the value x = 2 in the expressions for the dimensions found in point (2), we get:
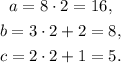
(4) Replacing the dimensions from point (3) in the expression for the volume, we get:
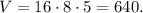
Which is the same result that we get in point (2), as it should be.
Answer
(1) Dimensions
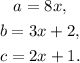
(2) Volume when x = 2:
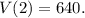
(3) Dimensions when x = 2:
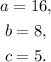
(4) Volume when x = 2: