Question

At a distance of 1 m, the intensity level of a soft whisper is about 30 dB, while a normal speaking voice is about 60 dB. How many times greater is the power delivered per unit area by a normal speaking voice than by a whisper?

Answer 1

The sound intensity level is defined as:

`L=10\log _(10)((I)/(I_0))dB`

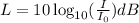
Where dB is decibel, I₀ is the reference sound intensity (commonly 1 pW/m²) and I is the intensity of the sound wave. The intensity of a sound is the same as the power delivered per unit area.

Isolate I from the equation:

`I=I^{}_0\cdot10^{(L)/(10dB)}`

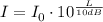
To compare the intensities of two sounds, consider I₁ and I₂ and find the ratio between them:

`\begin{gathered} I_1=I^{}_0\cdot10^{\frac{L_1_{}_{}}{10dB}} \\ I_2=I^{}_0\cdot10^{(L_2)/(10dB)} \end{gathered}`

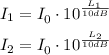
Then:

`\begin{gathered} (I_1)/(I_2)=\frac{I^{}_0\cdot10^{\frac{L_1_{}_{}}{10dB}}}{I^{}_0\cdot10^{(L2)/(10dB)}} \\ =10^{(L_1-L_2)/(10dB)} \end{gathered}`

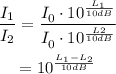
Use the subindex 1 to represent the speaking voice and the subindex 2 to represent the whisper. Substitute L₁=60dB and L₂=30dB to find how many times greater is the power delivered per unit area by a normal speaking voice than by a whisper:

`\begin{gathered} (I_1)/(I_2)=10^{(60dB-30dB)/(10dB)} \\ =10^{(30dB)/(10dB)} \\ =10^3 \\ =1000 \end{gathered}`

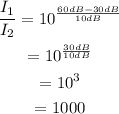
Therefore, the power delivered per unit area by a normal speaking voice is 1000 times greater than the power delivered per unit area by a whisper.