The sound intensity level is defined as:
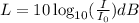
Where dB is decibel, I₀ is the reference sound intensity (commonly 1 pW/m²) and I is the intensity of the sound wave. The intensity of a sound is the same as the power delivered per unit area.
Isolate I from the equation:
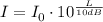
To compare the intensities of two sounds, consider I₁ and I₂ and find the ratio between them:
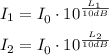
Then:
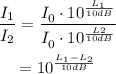
Use the subindex 1 to represent the speaking voice and the subindex 2 to represent the whisper. Substitute L₁=60dB and L₂=30dB to find how many times greater is the power delivered per unit area by a normal speaking voice than by a whisper:
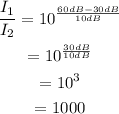
Therefore, the power delivered per unit area by a normal speaking voice is 1000 times greater than the power delivered per unit area by a whisper.