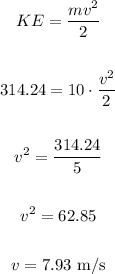Question

Calculatea: The work done by the boy on the mowerb: the work done on the friction force on the mowerc: the network don on the mowerd: the change in kinetic energy on the mowere: using energy method how much is the final velocity on the mower

Answer 1

First, let's calculate the horizontal component of the force applied by the boy:

`\begin{gathered} F_x=F\cdot\cos30°\\ \\ F_x=80\cdot0.866\\ \\ F_x=69.28\text{ N} \end{gathered}`

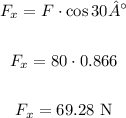
Now, let's calculate the works:

a.

The work done by the boy will use only the horizontal component of the force applied by the boy:

`\begin{gathered} W=F_x\cdot d\\ \\ W=69.28\cdot8\\ \\ W=554.24\text{ J} \end{gathered}`

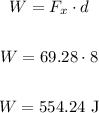
b.

The work done by the friction force uses only the friction force:

`\begin{gathered} W_f=F_f\cdot d\\ \\ W_f=-30\cdot8\\ \\ W_f=-240\text{ J} \end{gathered}`

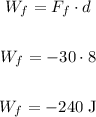
(We use a negative force because it is against the movement direction).

c.

The net work done on the mower is:

`\begin{gathered} W_(net)=W+W_f\\ \\ W_(net)=554.24-240\\ \\ W_(net)=314.24\text{ J} \end{gathered}`

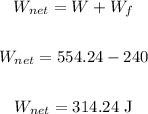
d.

The change in kinetic energy is equal to the net work, so it is equal to 314.24 J.

e.

Using the kinetic energy formula, we have:

`\begin{gathered} KE=(mv^2)/(2)\\ \\ 314.24=10\cdot(v^2)/(2)\\ \\ v^2=(314.24)/(5)\\ \\ v^2=62.85\\ \\ v=7.93\text{ m/s} \end{gathered}`