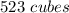Given the length (l), the width (w), and the height of the rectangular prism:
![\begin{gathered} l=7\operatorname{cm} \\ w=4\operatorname{cm} \\ \\ h=2(1)/(3)cm \end{gathered}]()
You can convert the height from Mixed Number to an Improper Fraction by multiplying the whole number part by the denominator and adding the result to the numerator. The denominator does not change:
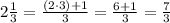
You need to use the following formula in order to calculate the volume of the rectangular prism:
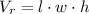
Where "l" is the length, "w" is the width, and "h" is the height.
Substituting values and evaluating, you get:
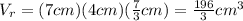
Now you need to find the volume of a cube using this formula:
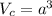
Where "a" is the length of one edge.
In this case:
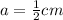
Therefore:
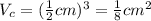
Let be "x" the number of cubes needed to fill the rectangular prism. Notice that:
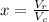
Then:
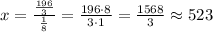
Hence, the answer is: