Question

Determine the maximum or minimum value of the function. f(x) = 6x^2-x-4

Answer 1

This is an equation of a parabola (quadratic) of the form:

`ax^2+bx+c`

According to the equation, the values of the constants are:

a = 6

b = -1

c = -4

The max value of a parabolic function occurs at:

`x=-(b)/(2a)`

We substitute and find:

`\begin{gathered} x=-(-1)/(2(6)) \\ x=(1)/(12) \end{gathered}`

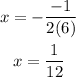
Then, if u plug in that number into the function, you will get the max/min value:

`\begin{gathered} f((1)/(12))=6((1)/(12))^2-(1)/(12)-4 \\ =6((1)/(144))-(1)/(12)-4 \\ =(1)/(24)-(1)/(12)-4 \\ =(1-1(2)-4(24))/(24) \\ =(1-2-96)/(24) \\ =-(97)/(24) \end{gathered}`

So, the extrema value is at:

`((1)/(12),-(97)/(24))`

Also, this is a minimum.

If a > 0 , we have a minimum

If a < 0, we have a max.

Since a = 6 which is greater than 0, so the answer is minimum.