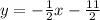Question 1.
Given the point:
(-3, -4)
Slope, m = - 1/2
Let's write the equation of the line that passes through the given point with the slope in point-slope form and slope intercept form.
• Point slope form:
Apply the point-slope equation:

Now substitute -1/2 for m, then input (-3, -4) for x1 and y1 in the equation above.
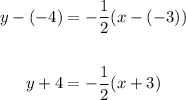
Therefore, the equation in point slope form is:
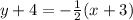
• SLope intercept form:
Apply the slope intercept form of a linear equation:

Where m is the slope and b is the y-intercept.
Substitute the following:
-1/2 for m
(-3, -4) for (x, y)
Then solve for b.

Subtract 3/2 from both sides:
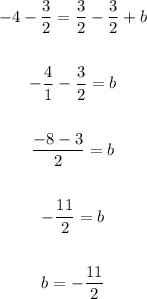
Therefore, the slope intercept form of the line is:
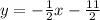
ANSWER:
Point-slope form:
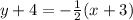
Slope intercept form: