Question

A city currently has 130 streetlights. As part of a urban renewal program, the city council has decided to install 2 additional streetlights at the end of each week for the next 52 weeks.How many streetlights will the city have at the end of 40 weeks?

Answer 1

Since the increment of number of lights is constant we can model the number of lights with a linear equation; we know that the line with slope (or rate of change) m and y-intercept b is given by:

`y=mx+b`

In this case, the slope of the line will be 2 and the y-intercept is 130; hence the number of lights in any week is given by:

`y=2x+130`

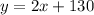
Now that we have an expression we can plug the week we want to know to determine the number of lights, since we want to know the number of lights at the end of week 40 we have that x=40; then:

`\begin{gathered} y=2(40)+130 \\ y=80+130 \\ y=210 \end{gathered}`

Therefore, at the end of week forty there will be 210 lights.