Question

Find the surface area of the figure.Assume the cylinder is closed at both ends. Use 3.14 for π and round to the nearest hundredth, if necessary.

Answer 1

Assuming the cylinder is closed at both ends, the surface area of the figure is equal to 150.72 square miles.

In Mathematics and Geometry, the surface area of a cylinder can be calculated by using this mathematical equation (formula):

Surface area of a cylinder, SA = 2πrh + 2π
`r^2`

Where:

• h represents the height.
• r represents the radius.

By substituting the given parameters into the formula for the surface area (SA) of a cylinder, we have the following;

Surface area of a cylinder, SA = 2πrh + 2π
`r^2`

Surface area of a cylinder, SA = (2 × 3.14 × 3 × 5) + 2 × 3.14 ×
`3^2`

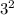
Surface area of a cylinder, SA = 94.2 + 56.52

Surface area of a cylinder, SA = 150.72 square miles.

Answer 2

The surface area of a cylinder is the sum of the lateral area and the area of both ends (or lids).

The surface area can be calculated with the formula:

`SA=2\pi r^2+2\pi rh`

Where r is the radius and h is the height.

The cylinder drawn in the figure has r=3 mi and h=5 mi.

Applying the formula:

`\begin{gathered} SA=2\cdot3.14\cdot3^2+2\cdot3.14\cdot3\cdot5 \\ SA=150.72mi^2 \end{gathered}`

The surface area of the figure is 150.72 square mi