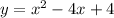We can solve this problem using two equations, one quadratic, and one linear, such as the graphs have no point in common, that is, both graphs have no common points or intersections between them. Therefore, we can use the following equations:
1. Quadratic equation: we can have one equation shifted to the right 2 units:
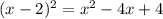
2. Now, we can use a line equation so that it does not pass through the quadratic equation. Since most of the quadratic equation is in the first quadrant, we can use a line with a negative slope. We can use the x-intercept equal to (-2, 0), and (0, -2). For this, we can find the slope for this line:
x1 = -2
y1 = 0
x2 = 0
y2 = -2
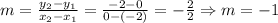
Applying the point-slope form of the line, we have:
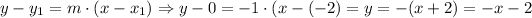
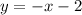
Then, we have that the system of equation is:
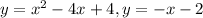
If we graph both equations, we have the following graph:
Since we can see that both graphs will never intersect each other, we can conclude that this system does not have solutions in the Real set of numbers.
The linear equation is:
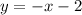
The quadratic equation is: