Given the rational expression below:
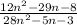
The simplification is as shown below:
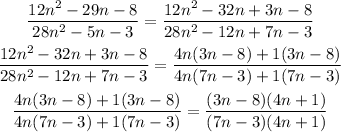
It can be observed from the simplification that (4n+1) is common to both the numerator and denominator. To simplify further we will cross (4n+1) out in the numerator and denominator as shown below:
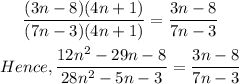
Hence, after the simplification,
the numerator is 3n - 8, and
The denominator is 7n - 3