Let's first draw the scenario to better understand the problem:
In this scenario, we will be using the Pythagorean Theorem.
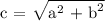
In this scenarios, the equation will be:
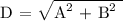
Let's find dD/dt,
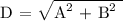
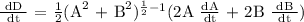
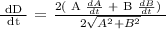
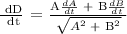
After 3 hours,
A = 20 + 17(3) = 20 + 51 = 71 knots
B = 21(3) = 63 knots
Let's find D,
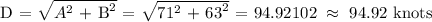
Let's now find dD/dt,
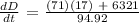
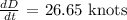
Therefore, the answer is 26.65 knots.