Question

At noon, ship A is 20 nautical miles due west of ship B. Ship A is sailing west at 17 knots and ship B is sailing north at 21 knots. How fast (in knots) is the distance between the ships changing at 3 PM? (Note: 1 knot is a speed of 1 nautical mile per hour.)

Answer 1

Let's first draw the scenario to better understand the problem:

In this scenario, we will be using the Pythagorean Theorem.

`\text{ c = }\sqrt{\text{a}^2\text{ + b}^2}`

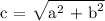
In this scenarios, the equation will be:

`\text{ D = }\sqrt{\text{A}^2\text{ + B}^2\text{ }}`

Let's find dD/dt,

`\text{ D = }\sqrt{\text{A}^2\text{ + B}^2\text{ }}`
`\text{ }\frac{\text{ dD }}{\text{dt}}\text{ = }(1)/(2)(\text{A}^2\text{ + B}^2)^{(1)/(2)-1}(2\text{A}^\text{ }\frac{\text{dA}}{\text{dt}}\text{ + 2B}^\text{ }\frac{\text{ dB }}{\text{ dt }})`
`\text{ }\frac{\text{ dD }}{\text{ dt }}\text{ = }\frac{2(\text{ A }(dA)/(dt)\text{ + B }(dB)/(dt))\text{ }}{2√(A^2+B^2)}`
`\text{ }\frac{\text{ dD}}{\text{ dt}}\text{ = }\frac{\text{A}(dA)/(dt)\text{ + B}(dB)/(dt)}{\sqrt{A^2\text{ + B}^2}}`

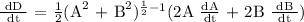
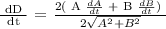
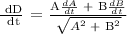
After 3 hours,

A = 20 + 17(3) = 20 + 51 = 71 knots

B = 21(3) = 63 knots

Let's find D,

`\text{ D = }\sqrt{A^2\text{ + B}^2}\text{ = }\sqrt{71^2\text{ + 63}^2}\text{ = 94.92102 }\approx\text{ 94.92 knots}`

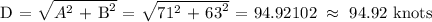
Let's now find dD/dt,

`(dD)/(dt)\text{ = }\frac{(71)(17)\text{ + \lparen63\rparen\lparen21\rparen}}{94.92}`
`\text{ }(dD)/(dt)\text{ = 26.65 knots}`

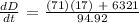
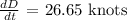
Therefore, the answer is 26.65 knots.