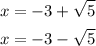Question

Solve using the quadratic formula x(x+6)+4=0

Answer 1

Step 1. The equation that we have is:

`x(x+6)+4=0`

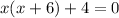
Before we apply the quadratic formula to solve the equation, we need to simplify the expression and multiply x by (x+6):

`\begin{gathered} x(x+6)+4=0 \\ \downarrow \\ x^2+6x+4=0 \end{gathered}`

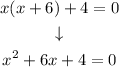
Step 2. The next step is to compare our equation with the general standard form of the quadratic equation:

`ax^2+bx+c=0`

And we find that the values of x, b, and c are:

`\begin{gathered} x^(2)+6x+4=0 \\ \downarrow\downarrow \\ a=1 \\ b=6 \\ c=4 \end{gathered}`

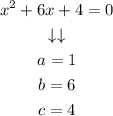
Step 3. We will use to values of a, b, and c in the quadratic formula:

`x=(-b\pm√(b^2-4ac))/(2a)`

Substituting the known values:

`x=(-6\pm√(6^2-4(1)(4)))/(2(1))`

Step 4. Solving the operations step by step:

`\begin{gathered} x=(-6\pm√(36-16))/(2) \\ \downarrow \\ x=(-6\pm√(20))/(2) \end{gathered}`

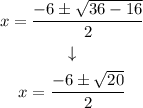
We can simplify the square root of 20 as follows:

`√(20)=√(4\cdot5)=2√(5)`

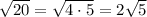
Therefore:

`x=(-6\pm2√(5))/(2)`

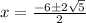
Now we make the division by 2:

`\begin{gathered} x=(-6\pm2√(5))/(2) \\ \downarrow \\ x=-3\pm√(5) \end{gathered}`

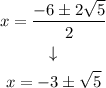
Step 5. The final step is to use the + and - signs to find our two solutions:

`\begin{gathered} Solution\text{ 1:} \\ x=-3+√(5) \\ Solution\text{ 2:} \\ x=-3-√(5) \end{gathered}`

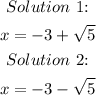
Answer:

`\begin{gathered} x=-3+√(5) \\ x=-3-√(5) \end{gathered}`