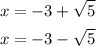Step 1. The equation that we have is:
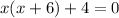
Before we apply the quadratic formula to solve the equation, we need to simplify the expression and multiply x by (x+6):
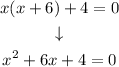
Step 2. The next step is to compare our equation with the general standard form of the quadratic equation:

And we find that the values of x, b, and c are:
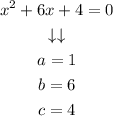
Step 3. We will use to values of a, b, and c in the quadratic formula:
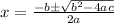
Substituting the known values:
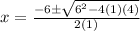
Step 4. Solving the operations step by step:
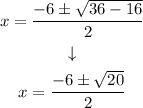
We can simplify the square root of 20 as follows:
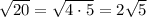
Therefore:
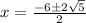
Now we make the division by 2:
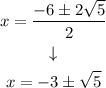
Step 5. The final step is to use the + and - signs to find our two solutions:
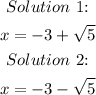
Answer: