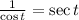ANSWER
= sec(t)
Step-by-step explanation
First let's rewrite this in terms of sines and cosines:
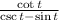
The cotangent is the reciprocal of the tangent:
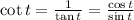
And the cosecant is the reciprocal of the sine:
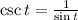
Replace into the given expression:
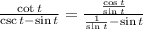
We can add the two terms in the denominator:
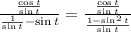
The denominators of each fraction get cancelled out:

We still can simplify this a little further. Remember the identity:
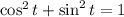
If we solve it for cos²t:

We have the same expression of the denominator. So let's replace the denominator by cos²t:
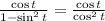
Simplify the square:
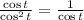
And this is the secant of t: