Let x be the length of the call per minute;
Let n be the cost per minute (in pence);
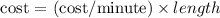
That is, at 12:30pm;
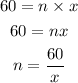
Similarly at 1:00pm;
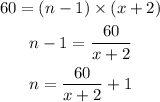
Then, we have expressed n in terms of x at 12:30pm and 1:00pm, then we have;
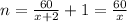
Simplifying further, we have;
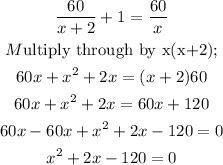
Thus, the equation is correct.
(iii) By simplifying the equation above, we have;
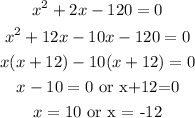
Thus, the length of Jane's call is 10minutes