Question

At 12:30 pm Jane made a telephone call which cost 60 pence. If she had waited until after 1:00 pm she could have had 2 minutes longer for the same cost. Calls after 1:00 pm are 1 penny per minute cheaper than calls before 1:00 pm. Let x minutes be the length of the call and n pence be the cost per minute at 12:30. i Express n in terms of x.ii Show that x + 2x - 120 = 0. iii Solve this equation and hence find the length of Jane's call.

Answer 1

Let x be the length of the call per minute;

Let n be the cost per minute (in pence);

`\begin{gathered} \text{ cost = (cost/minute)}* length \\ \end{gathered}`

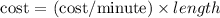
That is, at 12:30pm;

`\begin{gathered} 60=n* x \\ 60=nx \\ n=(60)/(x) \end{gathered}`

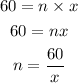
Similarly at 1:00pm;

`\begin{gathered} 60=(n-1)*(x+2) \\ n-1=(60)/(x+2) \\ n=(60)/(x+2)+1 \end{gathered}`

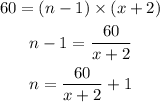
Then, we have expressed n in terms of x at 12:30pm and 1:00pm, then we have;

`n=(60)/(x+2)+1=(60)/(x)`

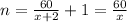
Simplifying further, we have;

`\begin{gathered} (60)/(x+2)+1=(60)/(x) \\ M\text{ultiply through by x(x+2);} \\ 60x+x^2+2x=(x+2)60 \\ 60x+x^2+2x=60x+120 \\ 60x-60x+x^2+2x-120=0 \\ x^2+2x-120=0 \end{gathered}`

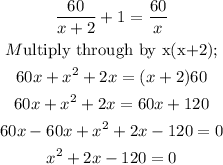
Thus, the equation is correct.

(iii) By simplifying the equation above, we have;

`\begin{gathered} x^2+2x-120=0 \\ x^2+12x-10x-120=0 \\ x(x+12)-10(x+12)=0 \\ x-10=0\text{ or x+12=0} \\ x=10\text{ or x = -12} \end{gathered}`

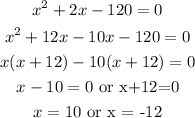
Thus, the length of Jane's call is 10minutes