ANSWER
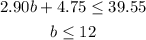
Step-by-step explanation
Each hamburger costs $2.90 and the hamburger roll costs $4.75
Let the number of hamburgers bought be b.
This means that b hamburgers cost:
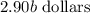
Mario has $39.55 to spend.
Therefore, the total cost of hamburgers and the hamburger roll must be less than or equal to $39.55.
That is:
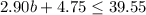
Now, solve for b in the inequality:
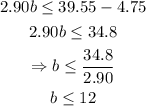
This means that Mario can afford to buy at most 12 hamburgers.