box1: y-axis
box2: dilation
box3:7
Step-by-step explanation
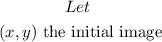
Step 1
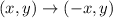
we can see y coordinate is the same, but x coordiante has opposite sign(its sign is changed)
hence
When you reflect a point across the y-axis, the y-coordinate remains the same, but the x-coordinate is transformed into its opposite (its sign is changed),so for box 1 the answer is
y-axis
Step 2
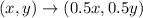
A dilation (similarity transformation) is a transformation that changes the size of a figure. It requires a center point and a scale factor , k
in this case k=0.5
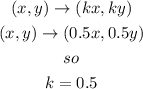
so, for box 2, the answer is dilation
Step 3

when you traslate horizontally , you affect the x coordinates, so

hence, in this case

and
when you traslate the figure vertically, you move on y axis, it means
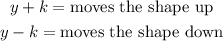
hence, in this case
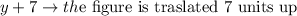
I hope this helps you