Question

A farmer wants to fence in 120,000 square feet of land in a rectangular plot and then divide it into two equal plots with another fence parallel to the short sides. What is the least amount of fence needed to accomplish this?

Answer 1

- The question says the area of the rectangular farmland is 120,000 square feet. This means that if the length is x and the breadth is y, then, the area can be represented as:

`\begin{gathered} x* y=120,000 \\ xy=120,000 \end{gathered}`

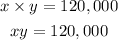
- Next, we are told that the land is to be divided in the middle by another fence into two equal halves. We are also told that the fence is parallel to the shorter side, implying that the larger side is the side is divided into two.

- Let us depict this last statement in the figure below:

- The length of fence needed is simply the length of the outer perimeter of the fence and also the length of the dividing fence. Thus, the length of fence needed can be expressed as follows:

`\begin{gathered} L=\text{ Perimeter of the Big Rectangle}+\text{ Length of the dividing fence} \\ L=2(x+y)+y \\ \text{ Expand,} \\ L=2x+2y+y \\ \\ \therefore L=2x+3y \end{gathered}`

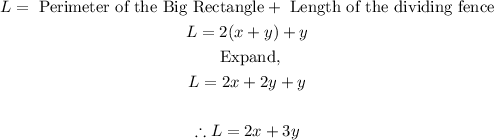
- This is an expression for the amount of fence needed by the question. Let us proceed to write this equation in terms of either x or y alone using the first equation

`\begin{gathered} \text{ From the first equation,} \\ y=(120,000)/(x) \\ \\ \text{ Thus, we have} \\ L=2x+3y \\ L=2x+3*(120,000)/(x) \\ \\ L=2x+(360,000)/(x) \end{gathered}`

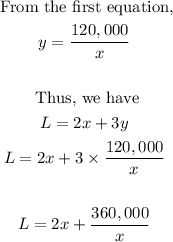
- We are asked to find the least amount of fence needed. In order to get this, we need to find the derivative of the function of L(x) with respect to x. After this, we equate that derivative to zero.

- The derivative represents the increase or decrease of the total material length (L) with respect to length (x)

- Equating that derivative to zero tells us that the change in those values has been completely minimized

- Thus, we have:

`\begin{gathered} L^(\prime)=2+(-1)(360,00)/(x^2) \\ \\ L^(\prime)=2-(360,000)/(x^2) \\ \\ \text{ Equate the derivative to zero} \\ \\ 2-(360,000)/(x^2)=0 \\ \\ \text{ Multiply through by }x^2 \\ \\ 2x^2-360,000=0 \\ \text{ Divide through by 2} \\ \\ x^2-180,000=0 \\ x^2=180000 \\ Take\text{ the square root of both sides} \\ \\ x=√(180,000)ft \\ OR \\ x=424.264ft \end{gathered}`

- Thus, if x = 424.264, then, we can find the least amount of fence needed by

`\begin{gathered} L=2x+(360,000)/(x) \\ \\ \text{ Put }x=424.264 \\ \\ L=2(424.264)+(360,000)/(424.264) \\ \\ \therefore L=1,697.056ft \end{gathered}`

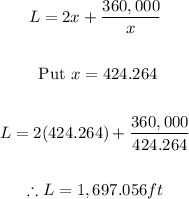
Final Answer

The least amount of fence required is 1697.056ft