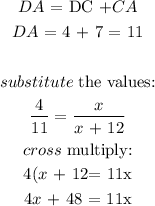Answer:
x = 6.9 (option D)
Step-by-step explanation:
Given:
DC = 4, CA = 7
CE = x, BA = x + 12
To find:
the value of x
To determine x, we will apply the similarity theorem for triangles:
For two triangles to be similar, the ratio of corresponding sides will be equal
Triangle EDC is similar to triangle BDA