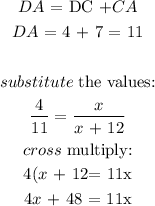Question

Find the value of x, given the image below.Select one:a.Cannot be determinedb.28c.16d.6.9

Answer 1

Answer:

x = 6.9 (option D)

Step-by-step explanation:

Given:

DC = 4, CA = 7

CE = x, BA = x + 12

To find:

the value of x

To determine x, we will apply the similarity theorem for triangles:

For two triangles to be similar, the ratio of corresponding sides will be equal

Triangle EDC is similar to triangle BDA

`\begin{gathered} DC\text{ corresponds to DA} \\ CE\text{ corresponds to AB} \\ \\ The\text{ ratio:} \\ (DC)/(DA)\text{ = }(CE)/(AB) \end{gathered}`
`\begin{gathered} DA\text{ = DC +}CA \\ DA\text{ = 4 + 7 = 11} \\ \\ substitute\text{ the values:} \\ (4)/(11)=\frac{x}{x\text{ + 12}} \\ cross\text{ multiply:} \\ 4(x\text{ + 12\rparen = 11\lparen x\rparen} \\ 4x\text{ + 48 = 11x} \end{gathered}`
`\begin{gathered} collect\text{ like terms:} \\ 48\text{ = 11x - 4x} \\ 48\text{ = 7x} \\ \\ divide\text{ both sides by 7:} \\ (48)/(7)\text{ = }(7x)/(7) \\ x\text{ = 6.857} \\ \\ x\text{ = 6.9 \lparen1 decimal place\rparen \lparen option D\rparen} \end{gathered}`