Question

A scuba diver is exploring a coral reef at a depth of 15.2 meters below the surface of a (fresh water) lake. Calculate the absolute pressure (in kilopascals) experienced by the diver. Assume that atmospheric pressure is 101,000 Pa=101 kPa. If this diver discovers a solid aluminum bar with dimensions of 0.520 m by 0.540 m by 0.950 m, calculate the buoyant force experienced by the bar.

Answer 1

Given data

*The given depth is h = 15.2 m

*The given atmospheric pressure is P_atm = 101 kPa

*The value of the density of freshwater is D_w = 1000 kg/m^3

*The value of the acceleration due to the gravity is g = 9.8 m/s^2

The expression for the absolute pressure (in kilopascals) experienced by the diver is given as

`P_(abs)=P_(atm)+D_wgh`

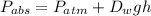
Substitute the known values in the above expression as

`\begin{gathered} P_(abs)=101+(1000*9.8*15.2) \\ =101+(148960\text{ Pa)} \\ =101\text{kPa}+148.96\text{ kPa} \\ =249.6\text{ kPa} \end{gathered}`

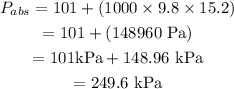
Hence, the absolute pressure (in kilopascals) experienced by the diver is P_abs = 249.6 kPa

As from the given data, the dimension of a solid aluminum bar is 0.520 m by 0.540 m by 0.950 m, then the buoyant force experienced by the bar is calculated as

`F_b=D_wVg`

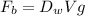
*Here V is the volume of the bar

Substitute the known values in the above expression as

`\begin{gathered} F_b=(1000)(0.520*0.540*0.950)(9.8) \\ =2614.24\text{ N} \end{gathered}`

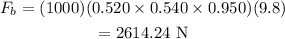
Hence, the buoyant force experienced by the bar is F_b = 2614.24 N