The converse of Basic Proportionality Theorem: If a line divides any two sides of a triangle in the same ratio, then the line must be parallel to the third side.
From the sketch,
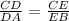
Take the reciprocal
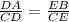
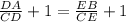
Any number divided by itself is 1, so we can replace 1 with CD/CD or CE/CE
so that
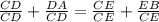
Combine terms using our common denominator
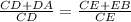
from the diagram, we can see that
CA=CD+DA
and
CB=CE+EB
Then

Since the triangles have SAS for triangle similarity.
This means that
