Question

Look at the system of equations shown in the graph. What is the solution to the system?

Answer 1

A solution to a system of linear equations is the point of intersection of both lines when graphed.

Parallel lines do not ever cross so there are zero solutions.

However, there could be a chance that there is a solution because often, the equation of two lines that look parallel are actually the same line, in which case the system will produce an infinite number of solutions.

The way to be sure is just to pick an x value randomly and put it in both equations and see if the answers are equal. If it is really two parallel lines, they will not be equal otherwise, they will be equal.

Hence from the graph, we will first get the equation for both lines

Line 1

`\begin{gathered} y_2=-4 \\ y_1=2 \\ x_2=0 \\ x_1=-2 \\ \text{Hence the equation of the line is given as} \\ y-y_1=(y_2-y_1)/(x_2-x_1)(x-x_1)_{} \end{gathered}`
`\begin{gathered} y\text{ -(2)=}\frac{-4-(2)_{}}{0-(-2)}(x-(-2)) \\ y-2=(-6)/(2)(x+2) \\ y-2\text{ = -3x}-6 \\ y\text{ = -3x -}6+2 \\ y\text{ = -3x-4} \end{gathered}`

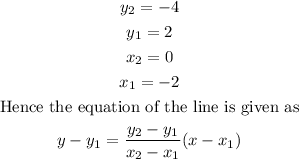
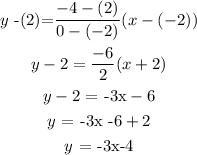
For line 2

`\begin{gathered} y_1=4 \\ y_2=\text{ 1} \\ x_2=0 \\ x_1=-1 \\ \text{The equation of the line is} \\ y-y_1=(y_2-y_1)/(x_2-x_1)(x-x_1) \\ \text{After susbstitution} \\ y\text{ -4=}(1-4)/(0-(-1))(x-(-1)) \\ y-4\text{ = }(-3)/(1)(x+1) \\ y-4=-3x-3 \\ y\text{ = -3x-3+4} \\ y\text{ = -3x+1} \end{gathered}`

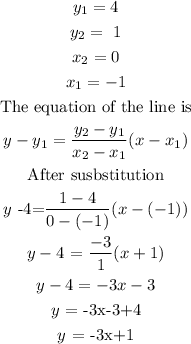
So picking a random value of x= -1

we will have

`\begin{gathered} \text{Line 1} \\ y\text{ = -3(-1)-4} \\ y=3-4 \\ y\text{ = -1} \\ \text{Line 2} \\ y\text{ = -3(-1)+1} \\ y=\text{ 3+1} \\ y\text{ =4} \end{gathered}`

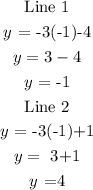
Since both values of y using a constant random value of x gives us different answers, the lines, therefore, are not images of each other and the system has no solution.

Final answer------ No solution