For this problem, we are asked to provide the intermediate step we obtain while completing the square for the following expression:
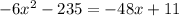
Completing the square means to transform the function into a expression such as:
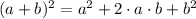
For this we will first change all the terms to the left side, as shown below:
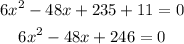
Since all three terms are divisible by 6, we need to use factorization to isolate the 6 from the equation:

Now, we need to rewrite the expression inside the parenthesis, such as we will obtain a form that is roughly equal to the perfect square we're looking for.
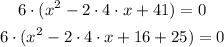
Now, we need to remove the "25" from the parenthesis, for that we need to multiply the 6 by 25.
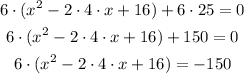
Now we can transform the parenthesis to the sum of two squares, where the term "a" is equal to x, and the "b" is equal to 4.
