Question

If mAB = 72 degree, find the area of shaded sector AOB, in terms of pi

Answer 1

If mAB = 72 degrees, then the central angle O will have the same measure.

Now, to find the sector area of a circle, we use the next equation:

`\frac{central\text{ angle}}{360}=(sector)/(\pi r^2)`

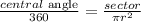
Where :

r = radius = 10

O = Central angle = 72 degrees.

Solve for the area of the sector AS:

`AS=\frac{central\text{ angle}}{360}\ast\pi r^2`

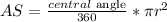
Replacing:

`AS=(72)/(360)\ast\pi(10)^2`

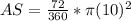
Solve it:

`AS=20\pi`

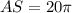
Hence, the area of the vector is 20π.