We count the total number of possibilities for the area codes in the next manner:
1. For the first digit of the codes, we have six options, these are; 3,4,5,6,7,8
2. For the second digit of the codes, three options\; 2,3,4
3. For the third digit of the codes with can put any digit number except 6,7 or 8, that restriction let us the following possibilities:0,1,2,3,4,5,9
We will use the multiplicative rule to count the total number of possible codes with this restrictions, that is we will apply a rule of the form:
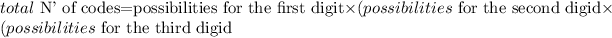
In our the specific case

Therefore, we conclude that with these restriction, the total number of codes is 126