ANSWER
height = 80in
width = 30 in
Step-by-step explanation
The perimeter of the door is the sum of twice the width and twice the height:
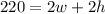
We also know that the width is 50in less than the height:
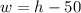
Replace w by this equation into the perimeter:
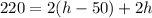
Solve for h. Apply distributive property:
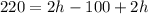
Add like terms:
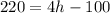
Add 100 to both sides of the equation
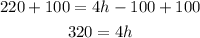
Divide both sides by 4
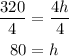
The height of the door is 80 in.
Now replace h = 80 into the equation of the width of the door:

The width of the door is 30 in.