Question

the distribution of heights of adult American men is approximately normal with mean 68 in and a standard deviation of 2.5 in what percent of men are between 63 and 73 ?

Answer 1

Let x be a random variable representing the heights of adult American men. Since it is normally distributed and the population mean and standard deviation are known, we would apply the formula,

z = (x - mean)/Standard deviation

From the information given,

mean = 68

standard deviation = 2.5

The probability that the height of a selected adult is between 63 and 73 is expressed as

`P(68\leq x\leq73)`

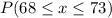
For x = 63,

z = (63 - 68)/2.5 = -2

Looking at the normal distribution table, the probability corresponding to the z score is 0.02275

For x = 73,

z = (73 - 68)/2.5 = 2

Looking at the normal distribution table, the probability corresponding to the z score is 0.97725

Therefore,

`P(68\text{ }\leq x\leq73)\text{ = 0.97725 - 0.0}2275\text{ = 0}.9545`

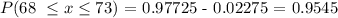
Thus, the percentage of men are between 63 and 73 is

0.9545 * 100 = 95.45%

Rounding up to the nearest percentage, the answer is 95%