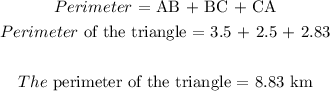Answer:
The perimeter of the triangle is 8.83 km
Step-by-step explanation:
Given:
2) Triangle ABC with sides AB, BC and CA
To find:
The perimeter of the triangle using the distance formula
To determine the perimeter, we need to first find the 3 sides of the triangle. To do this, the distance formula will be used:
![$$dis\tan ce\text{ = }\sqrt[]{(y_2-y_1)^2+(x_2-x_1)^2}$$](https://img.qammunity.org/2023/formulas/mathematics/college/h7u7esjqrnm3xx7e2nlhkc49adzfswxk3z.png)
A = (0, 0), B = (3.5, 0) and C = (2, -2)
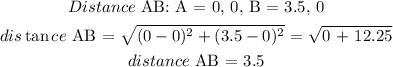

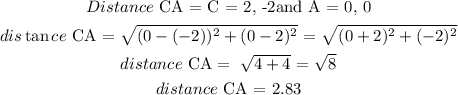
The perimeter of the triangle = sum of all 3 sides