Question

If the measure of angle GAT equals 30° in GT equal 60 cm, find GA & AT.

Answer 1

As a result of crossing the rectangle from one vertex to the opposite vertex we get a right triangle, like this:

With right triangles, we can use the trigonometric ratios:

`\begin{gathered} \sin \theta=(oc)/(h) \\ \cos \theta=(ac)/(h) \end{gathered}`

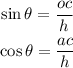
Where h is the length of the hypotenuse of the triangle, oc is the opposite leg and ac is the adjacent leg.

By taking θ as the angle whose measure equals 30°, we get:

`\begin{gathered} \sin \theta=(GT)/(GA) \\ \cos \theta=(AT)/(GA) \end{gathered}`

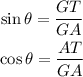
From the sine function, we can replace 30° for θ and 60 for GT, then solving for GA, we get:

`\begin{gathered} \sin 30=(60)/(GA) \\ \sin 30* GA=(60)/(GA)* GA \\ \sin 30* GA=60*(GA)/(GA) \\ \sin 30* GA=60*1 \\ \sin 30* GA=60 \\ (\sin30)/(\sin30)* GA=(60)/(\sin30) \\ 1* GA=(60)/(\sin30) \\ GA=(60)/(\sin30) \\ GA=120 \end{gathered}`

Then, GA equals 120 cm.

Similarly, by means of the trigonometric function cosine, we get:

`\begin{gathered} \cos 30=(AT)/(120) \\ \cos 30*120=(AT)/(120)*120 \\ \cos 30*120=AT*(120)/(120) \\ \cos 30*120=AT*1 \\ AT=\cos 30*120 \\ AT=60\sqrt[]{3} \end{gathered}`

Then the side AT has a length of 60√3 cm (about 104 cm)