As a result of crossing the rectangle from one vertex to the opposite vertex we get a right triangle, like this:
With right triangles, we can use the trigonometric ratios:

Where h is the length of the hypotenuse of the triangle, oc is the opposite leg and ac is the adjacent leg.
By taking θ as the angle whose measure equals 30°, we get:
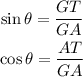
From the sine function, we can replace 30° for θ and 60 for GT, then solving for GA, we get:

Then, GA equals 120 cm.
Similarly, by means of the trigonometric function cosine, we get:
![\begin{gathered} \cos 30=(AT)/(120) \\ \cos 30*120=(AT)/(120)*120 \\ \cos 30*120=AT*(120)/(120) \\ \cos 30*120=AT*1 \\ AT=\cos 30*120 \\ AT=60\sqrt[]{3} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/2cne9v4a16igehdthrseuj50gn7yvgrav6.png)
Then the side AT has a length of 60√3 cm (about 104 cm)