Take into account that triangles FGH and GKJ are similar. Then, you can write the following equivalence between the lengths of similar sides:
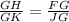
where,
GH = ?
GK = 6
FG = 7 + 4 = 11
JG = 4
Solve for GH, replace the values of the other parameters and simplify:
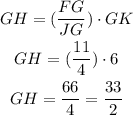
Now, take into account that:
GH = GK + KH
Solve for KH, replace the values of GH and GK and simplify:
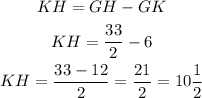
Hence, the lngth of KH is 10 1/2